HDRP裡光源的單位

➡️ 目錄

功率Power

W(瓦特)、Φλ(radianet flux)都是功率

Hz頻率

量綱為 1/s

SPD(λ)

SPD → spectral power distribution

More generally, the term SPD can refer to the concentration, as a function of wavelength, of any radiometric or photometric quantity (e.g. radiant energy, radiant flux, radiant intensity, radiance, irradiance, radiant exitance, radiosity, luminance, luminous flux, luminous intensity, illuminance, luminous emittance).

SPD量綱可以是 E / λ、L / λ、I / λ、Φ / λ

λ是波長

備註

知道機率和機率密度有什麼不同後

我終於get到SPD為什麼要這麼定義

Book5_Ch02_统计描述__统计至简__鸢尾花书 💫

PBR 5.1 Spectral Representation

SPD(λ)轉RGB

SPD

是怎麼轉成 RGB的？

出處

出處

SI的cd

原來就是 I 阿 😋🤠 有眼不識泰山

Wiki

Photometry
W和lm不一樣

Photometry

Photometry → 光度學

不同於Radiometry

光度學把不同波長的Φ_λ用光度函數加權

合成對人眼的有效Φ_v (Luminous flux)

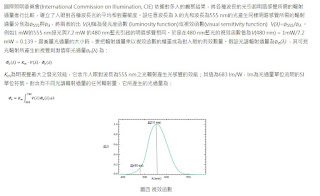
Φ_v = K_555.016 ∫ V(λ) Φ_e(λ) dλ

K_555.016 = 683 lm / W

光強度的單位：燭光(cd)

不只對Φ可以

也能轉換I_e為I_v

以此類推

光強度的單位：燭光(cd)

來看看Unity裡的單位

HDRP裡光源的單位是Photometry  ❓

EV 100 查了一下是光圈，和針孔相機的孔徑大小有關

Lux是用 E = I / (R²)，R = 1算出來的

Hello HDRP

看了這系列的文章發現

📑 [总结] 漫谈HDR和色彩管理（五）游戏中的HDR

光源的單位直接使用Photometry

對SDR銀幕 
渲染完得到的nit (N_x , N_y , N_z)
經過如此如此這般這般…
最後RGB會落在0~1之間
銀幕再根據RGB決定要顯示多亮(nit)

對HDR銀幕 
渲染完得到的nit (N_x , N_y , N_z)
經過如此如此這般這般…
最後RGB也會落在0~1之間
銀幕再根據RGB決定要顯示多亮(nit)

from unity HDRP Color.hlsl

完成Tonemapping後
會把(N_x , N_y , N_z)重新映射到(R , G , B)
R、G、B會位在0~1之間

RGB和銀幕的L_max

當pixel的RGB=(1,1,1)

會得到銀幕的最大nit值L_max

當pixel的RGB=(0.5,1,1)

得到的銀幕nit值 < L_max

光源強度L_v和color filter

有面光源

color filter = (r,g,b) 和 Luminance = L_v

指的是

當color filter為(1 , 1 , 1)時面光源Luminance = L_v

color filter調小後，面光源Luminance < L_v

Unity HDRP 的面光源 

L = Φ / 4π / A 

單位選Lumen時

會固定Φ，所以把面光源面積調大A，L就會減弱 

單位選nit (L)時

會固定L，把面光源面積A調大，亮度不變，代表Φ增加了

點光源L的Error 👩‍🔬

➡️ 目錄

dE⊥

「dA是很小的面積」

dE⊥ = L * dω = L * dA / R² = dA I / R²    -式①

「1是1平方公尺的面積」

dE⊥十十  = L * 1m² / R² = I / R²    -式②

A_s

shading point A_s是很小的區域，面積只有dA

計算點光源的光照時

為什麼要使用dE⊥十十 = L * 1m² / R²

不是全部的能量只有部份到達dA_s嗎？

(見下面圖①)

 👩‍🔬 下篇：

• 點光源的謎團

面光源的I / (R*R)

➡️ 目錄

🚧 本篇存在符號的歧異

• 符號的歧異

Integrals over Area
E = ∫ dE
出處

使用蒙地卡羅積分

Lo = ( Σ BRDF * L_i * 幾何項 * (1 / pdf(i)) ) (1 / n) 

化簡幾何項

幾何項 = cos(θ_i)cos(θ_o) / R_i²

假設面光源正對shading point ΔA_s

且整個面光源對ΔA_s來說非常小時

R也可以當成一樣大

再利用平行的力量，cos(θ_i) = 1、cos(θ_o) =1

最後幾何項簡化成

幾何項 = 1 / R²

pdf

pdf(i) 是機率密度函數

最簡單的情況下 pdf(i) = 1 / A

1 / pdf(i) = A

使用diffuse

BRDF = 1 / π

Lo最後可以簡化為

L_o = ( Σ BRDF * L_i * 幾何項 ) (A / n)

L_o = ( Σ BRDF * ( L_i / R² ) ) (A / n)

L_o = BRDF * ( L_i / R² )  A

Lo = BRDF ( L_i A / R² ) = BRDF ( I / R² )     

如果是計算E_i

E_i = ( Σ  ( L_i / R² ) ) (A / n)

E_i = ( L_i / R² ) A

E_i =  L A  / R²

E_i = I / R² -式①

備註

當n的數量取得夠大

dA = (A / n)

L_o = ( Σ BRDF * ( L_i / R² ) ) (A / n)

L_o = ( Σ BRDF * ( L_i / R² ) ) dA

L_o = Σ BRDF * ( L_i / R² ) dA

( L_i dA / R² ) = dE

使用微小量

每1塊是

dE_i = cos(θ_i) cos(θ_o) L_i  dA / R²

使用前面的條件cos(θ_i) = 1、cos(θ_o) =1後有

dE_i = L_i  dA / R²

使用 Σ

一共有 (A / dA) 塊

count = (A / dA) 

count 可以不是整數

E_i = Σ dE_i = dE⊥_i * count

E_i = ( L_i dA / R² ) (A / dA) 

E_i = L_i  A / R² =  I / R² 

使用 ∫

E_i = ∫ dE_i = ∫ L_i  dA / R²  

E_i = (L_i / R²) ∫ dA

E_i = (L_i / R²) A = L_i A / R² = I / R²

半球積分的Li dωi ⭐

➡️ 目錄

而我低頭拆信 想知道關於L的事情 🎶

2年前

我被這個問題困惑 📧

「半球積分的dω不是要從光源的觀點思考？才能知道物體遠近嗎？」

吉人之辭寡 躁人之辭多

教授只是回覆我 📧

「渲染方程的dω是從shading point的觀點思考」

等等教授

你可以再說清楚一點嗎？

可是這樣怎麼知道物體的遠近？

經過2年的放置play後

我終於get到了

放置 play

BGM

渲染方程中

半球積分的 L_i dω_i 到底是什麼？

dω_i 到底是什麼？

思路1：模仿面光源

整片面光源對shading point P 的貢獻是 E

Integrals over Area
E = ∫ dE
出處

dω_i = cos(θ_o) dA / r ² 
dE⊥ = L dω_i
dE = cos(θ_i) L dω_i

從shading point dA發射射線

• ①擊中物體表面dA時，可以得到物體表面dA的L_o
• ②擊中光源表面dA時，可以得到光源表面L_o

但因為 dω = dA / R²

dω R² = dA

這個dA會覆蓋多個dA

所以記作 A = dA

可以把①也看成面光源

我們就可以模仿上面的Integrals over Area

使用平行的力量

上圖的L_i dω_i 其實是下圖上半部那種情況

用到的符號

• d平方

最左邊

L_i dω_i = dE⊥

Warning！

上述假設所有dA都會在一個平面上

但如果不是

而是有起伏的表面B怎麼辦？

C_o = cos(θ_o)不再是定值

但把構成B的dA沿著dω方向投影後

仍會得到平面A_p

∫ dA cos(θ_o) = A_p

dω = A_p / R²

思路2：直接使用 dω

不糾結於光源dA

只看shading point dA的dω取多大

由Received L的定義可知

dE⊥ = L dω

dω取愈大，dE⊥自然也愈大

考慮不同射入方向時自然有

dE_i = cos(θ_i) L dω_i

用思路2反推A的大小

已知 dE⊥ = L dω

又因為 dω = A C_o / R²

A = ∫ dA

當dω變大，代表有更多的dA對shading point貢獻dE⊥

補充

在半球積分時
光隨距離衰減，如何涌現

有1種path tracing 是不做直接光照

只靠Le來照亮場景

(L_e來自面光源P)

假設對shading point只計算1層

L_o  = L_e + ∫ F L_i cos(θ_i) dω_i 時

(不往下遞迴)

單看 L_o  = L_e + ∫ F L_i cos(θ_i) dω_i 這部分

_{當面光源P靠近shading point}

_{半球積分採樣到}的L_e多

_{反之，採樣到的Le少}

➡️ Geogebra