LTC Area Light 裡的線代

學微積分 也學人蔘 🤠

學Area Light 也學線代 🙂

前篇 ➡️ LTC Area Light

教材

Real-Time Polygonal-Light Shading with Linearly Transformed Cosines

進入主題

dω_o / dω 就叫Jacobian

paper的附錄A

paper的附錄A

附錄A的綠色框框？

M是Shearing Matrix
可以分解成
M = R^-1SR

式(17)怎麼來的？

好人1生平安

Cross product: matrix transformation identity

出處

粉紅色框框？

水藍色框框？

用幾何的方式來理解[ M ][ m ]

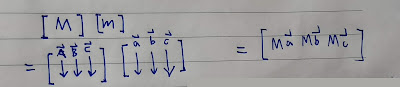M、m都是矩陣
[ M ]為矩陣M的行列式
[ m ]為矩陣m的行列式

[ M ] = 向量A、B、C張成的平行六面體體積
[ m ] = 向量a、b、c張成的平行六面體體積

符號的歧異

➡️ 目錄

⊥

覺得要特別標註⊥有點麻煩

之前都是直接信手拈來

Emitted L

• 交換微分順序的面光源Le ⭐⑫

E = dΦ / dA

L_o = dE_o / ( cos(θ_i) dω_o) 

L_o = dE_o / dω⊥_o 

📑 備註

這裡把dE_o寫成dE⊥_o 也不是不行

但∫ dE⊥_o = E，不是更怪？

加上dω⊥_o 就是投影立體角，用dE_o的話更一致

 

Received L

• Emitted L vs Received L ⭐⑭

dE⊥ = d²Φ / dA⊥ = d²Φ / (dA cos(θ_i))

L_i = dE⊥_i / dω_i 

cos(θ_i) dE⊥_i  = dE_i 

Integrals over Area
出處

最左邊

L_i dω_i = dE

最右邊

dω是固定的
進入dω的dΦ是固定的

中間
正面朝向的dA測量到的d²Φ大
傾斜朝向的dA測量到的d²Φ小

📑 備註
名為dE⊥
會讓人覺得光傾斜射入時
dA⊥一定會比dA小

但中間上方那張圖測量到的也是dE⊥
以這種視角，來看cos(θ_i) dE⊥_i  = dE_i
不是更加直觀？

Shading point

其實是個面

點光源

• 點光源的謎團 ⭐⑩

Shading point為dAs

E = I / R² 不一定會全部集中dAs

E_擊中dAs = cos(θ_i) I / R²

📑 備註
這裡也不是不能定義成
E⊥ = I / R²
但就覺得麻煩

BRDF

f = dL_o / dE_i

dE_i = cos(θ_i) dE⊥_i  = cos(θ_i) L_i dω_i 

f = L_o / E_i

E_i = E_擊中dAs

E_i = cos(θ_i) I / R²