看了這篇文章,很好奇為什麼
Support(v,-B) = (-1) * Support(-v,B)
於是就打開Geogebra玩看看
看了這篇文章,很好奇為什麼
Support(v,-B) = (-1) * Support(-v,B)
於是就打開Geogebra玩看看
如果你有1個正規化的4元數
q=(cos(θ/2),sin(θ/2) U)
q=(w,x,y,z)
這是它的共軛
q*=(cos(θ/2),-sin(θ/2) U)
q*=(w,-x,-y,-z)
要怎麼得到等效的旋轉矩陣呢?
如果是左乘的話 vM
那旋轉矩陣M就是
Xx Xy Xz
Yx Yy Yz
Zx Zy Zz
用四元數旋轉一個向量v
就是對向量v做三明治運算
q (0,v) q* = (0,v')
這樣得到的v'
就是v繞著U軸轉θ的結果
這是單位旋轉矩陣
X軸:1 0 0
Y軸:0 1 0
Z軸:0 0 1
分別對這3軸做1次三明治運算
q (0,X軸) q* = (0,X軸')
q (0,Y軸) q* = (0,Y軸')
q (0,Z軸) q* = (0,Z軸')
X軸'、Y軸'、Z軸'分別是
X軸、Y軸、Z軸繞U軸轉θ的結果
現在,你可以拿這個旋轉矩陣
X軸':? ? ?
Y軸':? ? ?
Z軸':? ? ?
來旋轉向量v了

|
| 第1種:MVP分開 |

|
| 第2種:MVP乘在一起 |

|
|
✖️是和y軸夾45度角的2個平面
(x , y , z , w)是Projection space的點
(1)畫的是(x , y , w)
(2)畫的是(x/w , y/w , 1)
(3)畫的是(x/w , y/w , z/w)
這張圖的NDC z是位在0~1之間
你會發現B的位置跑掉了
|

|
|
當三角形的2個頂點V0和V1需要被裁切
對線段做插值就可以得出裁切平面(遠平面)上的點
(視錐的其他5個平面也可以套用類似的方法)
|

|
|
圖 Screen Space
先解出t,s找到點hit,就能算出α
|
stacknavigator和tabnavigator
其實就是在處理狀態的轉移
所以用ASM就可以搞出一樣的效果
下面的狀態機是參考自這個頁面的UI配置
當時在練習使用Unity的UI ( 還不是為了 😍 錢錢
區塊代表的意義
如果1個程式是1個隨身碟;那usb插槽就是1個port
假設現在有隨身碟Server(S)、隨身碟Client(C)
UDP:
當要從S傳檔案A.txt到C,就要自己從S剪下,找到隨身碟C之後再貼上
(使用UDP,必須要提供另一端的ip和port)
TCP:
當C和S連線之後,會在S裡建立一個資料夾捷徑L(指到C裡的F資料夾)
當要從S傳檔案A.txt到C,只要剪下A.txt直接貼到L,這樣F裡就有A.txt了
(TCP在連線之後,已經記下了對方的ip和port)
TCP Sample Code
http://cs0.wikidot.com/chatbox
上面的程式碼
newsock.Bind(ipep);
newsock.Listen(10);
Socket client = newsock.Accept();
Socket client會設定2個port
localPort就是newsock使用的port (=20)
remotPort則是連進來的遠端程式使用的port
所以Accept得到的Socket並沒有佔用新的port
http://blog.csdn.net/tanyjin/article/details/69403220
WebSocket?
原來是因為:Server和Client是使用不同的port
比如說當程式和port 5555綁定
就可以透過5555來接收和傳送訊息;
但沒有限制一個程式只能和一個port綁定
https://zhidao.baidu.com/question
可以把sender的Port印出來,會發現它不是5555(而是發送端的port)
Console.WriteLine("Port:"+sender.Port);
(為了讓內網和外網的ip都可以被連到)
http://blog.csdn.net/farmer_worker
如何改成可以雙向傳送訊息?
Client-> Server
Server-> Client
Client也必須在1個port上綁定
這樣Server就知道要傳訊到那個port
發現比起用Socket,有個更方便的UDPClient
非同步版本的接收/發送
 |
| 如果你覺的這隻馬很面熟 對他叫熱鬥小馬,不是我原創的 |

|
|
Integrals over Area E = ∫ dE 出處 dωi = cos(θo) dA / r 2 dE⊥ = L dωi dE = cos(θi) L dωi |
 |
|
使用Lo = Lc * cos(θo) dEi =cos(θi) Lo dω dω = dA / Ri 2 也能推導出同樣的結果 |

|
|
半球積分裡多了 (1 / Ri 2) 項 🐞
|
|
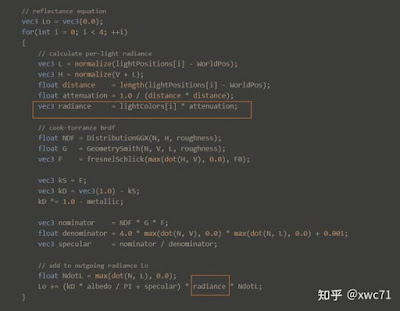
| 程式碼片段,來自LearnOpenGl CN 光照 |
➡️ 目錄

|
| 上圖來自advanced global illumination |

|
| Lc cos(θ) = dE / dω 式① |

|
|
reflectance即albedo(texture color) (13.9)就是render equation裡的半球積分 只考慮RGB其中1個component (且值為1) 有Diffuse BRDF為 F= 1 / π |