 |
|
因為L >> d 可以把r1和r2當成平行 這樣一來∠PQO也是θ |
 |
| 出處 |
 |
| 出處 |
試試看
能不能用解析幾何算出P的位置
 |
| ① 就是極座標,只是選了比較特別的軸向 ② S1A向量和 S2A向量垂直,相差90度 2個複數相乘 ⇔ 長度相乘,角度相加 |
 |
| 出處 |
 |
| 出處 水藍色的部分是修正項 這裡物理學家用括號
封裝座標變換的複雜度
|
 |
|
Jill的封裝
座標變換
從Jack座標系的r1變換到Jill座標系的r1'
從Jack座標系的r2變換到Jill座標系的r2'
算出dr' = r2' - r1', v' = dr' / dt 後
再把「v'」變換到Jack座標系的「v」
M的逆和M
Position和Vector不一樣
當輸入是Position
M的逆是4*4
M使用其中的3*3
當輸入是Vector
M的逆和M都是3*3
|
 |
| Jack的封裝 |
 |
| 出處 |
 |
| V的封裝只是依樣畫葫蘆 輸入都是Vector
M的逆和M都是3*3
|
 |
| 出處 Relation of V |
 |
| 出處 |
 |
| 出處 |
 |
| 老師的筆記 L15:Coriolis_effect 小粉紅為什麼可以變天空藍? |
 |
|
①M是線性變換
M ( d(M-1v) /
dt ) 對向量是線性變換 M的逆和M
當輸入是Vector
M的逆和M都是3*3
②地心就是Jack座標系的原點
位置r - 原點 = 向量r r是位置也是向量 ③正交矩陣對向量外積滿足分配律 M(axb) = Ma x Mb ( M的逆和M都是正交矩陣 ) 因為①②③ 把 (u + ω x r)
代入「Jill的封裝」
整理後
會得到和下圖同樣的結果
|
 |
| 整理的過程1 🧐 |
 |
| 整理的過程2 🧐 |
 |
| 出處 |
 |
| 出處 |
 |
| 出處 |
 |
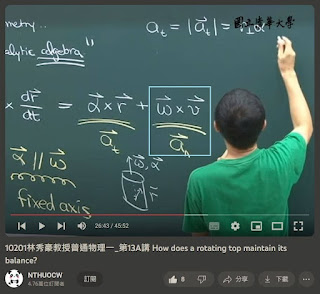
| 出處 即使是非等速圓周運動
向心力仍是 m a = m v v / r
|
 |
| 出處 |
 |
| 愛是折磨人的東西 卻又捨不得這樣放棄 🎶 |
 |
| BGM |
 |
| 出處 |
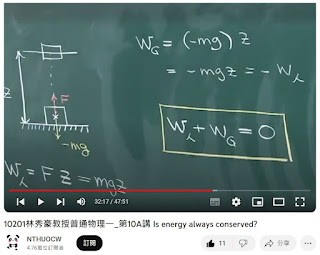 |
| 出處 慢慢把物體抬高z
重力作負功,人作正功,合為0
手放開
重力對物體作正功
物體的動能會增加
|
%201.JPG) |
| 出處 -ΔU移到等號右邊就變成了ΔU |
%202.JPG) |
| 出處 有了U之後
慢慢把物體抬高z
重力作的負功移到等號右邊,ΔU為正
手放開
重力對物體作正功
物體的動能增加ΔK
把重力作的正功移到等號右邊,ΔU為負
|
 |
|
還是從前那個小蓮
沒有一絲絲改變 🎶
|
 |
| 出處 宏觀
把子彈和方塊看成2個質點
DOF(自由度) = 2
內力是2個摩擦力在鬥法
|
 |
| 出處 宏觀
不存在外力時動量守恆
動量守恆則Vcm速度不變
Wnc是外力和內力的守恆力作的功
這個case只有內力(摩擦力)在作功
|
 |
| 出處 宏觀
摩擦力作工 = 質點內動能的減少
|
 |
| 出處 宏觀
減少的內動能跑去那了?
|
 |
| 出處 微觀
除了2個質點的動能
還包含其他小粒子的振動
|
 |
| 出處 微觀
摩擦力作功造成的動能減少
會讓其他小粒子的振動變強(動能增加)
一如以往面無表情 卻更洶湧
🎶
|
 |
| 出處 |
 |
| 出處 宏觀 VS 微觀
|