Hessian of h

愛拼才會贏 🎶

幾何二 第1講 

每日任務又出問題了？ 🤠

算不出老師說的K和H

我不開心 🙂

幾何二 第1講

當X(u , v) = ( u , v , h (u , v) )

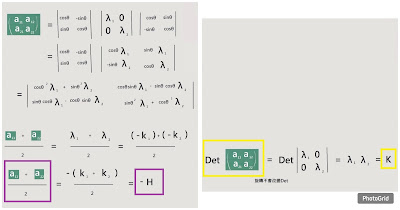
K和H會長這樣

K和H跟老師的不match

好 開始玩拼圖

當「X_u和X_v正交」而且 | X_u | = 1, |X_v| = 1
會有

• h_uv = f = 0 , e = k₁ , g = k₂
• EG - F² = 1
• E = 1, G = 1, F = 0

K和H跟老師的match了

再用 e 和 g 搭橋可以得到

• h_uu = k₁ , h_vv = k₂

小結

當「X_u和X_v正交」而且 | X_u | = 1, |X_v| = 1

有

• h_uu = k₁ , h_vv = k₂ , h_uv = f = 0

怎麼找出 z = h (u,v)

池同學的筆記

先做「泰勒展開」

假設 u=0, v=0 時

「X_u和X_v正交」而且 | X_u | = 1, |X_v| = 1

則有

• h_uu = k₁ , h_vv = k₂ , h_uv = f = 0

所以由「泰勒展開」得到的方程式為

z = (k₁ x² +  k₂ y²) / 2  

有了方程式

來檢驗看看

對任意點 h_uv = 0 ☑️ 

但除了

• u = 0 , v = 0
• u = 0 , v ≠ 0
• u ≠ 0 , v = 0

以外
其他Surface上的點都是「X_u和X_v不正交」

f 確實為 0

Geogebra

所有的X_u位在v = 0的平面上
所有的X_v位在u = 0的平面上

Geogebra

X_u只和水藍色曲線有關

不同v上的X_u只是水藍色曲線上X_u的平移

X_v只和紫紅色曲線有關

不同u上的X_v只是紫紅色曲線上X_v的平移

當選定1個v固定下來，X_v不變

沿著u方向，只有X_u和N會改變

N = X_u ^ X_v / | X_u ^ X_v |

但因為 N ⊥ X_v ( N不管怎麼變，都位和X_v垂直的平面上 )

所以會有 dN_p ( X_u ) ⊥ X_v

所以 - < dN_p ( X_u ) , X_v > = - < N_u , X_v > = f = 0 

所有X_u位在同1個平面上，X_v不變
最後所有N也會位在1個平面上

葡萄美酒夜光杯 欲飲琵琶馬上催

醉臥沙場君莫笑 古來征戰幾人回

你可知道 對我做過 什麼最殘忍

就是你 狠狠把我

一夜之間 變成了大人 🎶

雞蛋長大了 🤠🙂 雞蛋長大了

為什麼

假設 u=0, v=0 時

「X_u和X_v正交」而且 | X_u | = 1, | X_v | = 1

推出來的Surface方程式

h (u,v) = (k₁ u² +  k₂ v²) / 2 , 「f = h_uv = 0」

會存在「X_u和X_v不正交」的點

是不是因為？

「X_u和X_v正交」一定會「f = h_uv = 0」

但反過來

當「f = h_uv = 0」未必是因為「X_u和X_v正交」

好 來算算看dN

dN不是對稱矩陣

對稱矩陣的case

旋轉矩陣R可以看成1個正交座標系

上面就是A = RSR ^-1

R ^-1 V代表把V變換到Local space

當dN不是對稱矩陣

H、K和矩陣的關系還是不變

仍然可以用 第23講 的公式得到k₁ , k₂

對角化計算機

C和上面的R不一樣，C不是正交座標系
A = CSC ^-1

但2X2矩陣的特徵向量不正交
不代表3維的principal direction不正交

K和矩陣的關系不變

H和矩陣的關系不變

用 第23講 的公式得到k₁ , k₂

最大曲率 k₁(u,v) 
最小曲率 k₂(u,v) 

可視化

Geogebra

為了觀察方便

把height filed 移動了offset高

2個principal direction正交 (綠色和紅色直線)

是90度真是太好了 🤠🙂 用角角結束這1回合

回顧

切平面上一定存在1組正交的X₁和X₂

沿著X₁和X₂方向有最大曲率和最小曲率 (why)

by 歐拉 1760

X₁和X₂形成1個正交座標系

用③可以描述

沿著(a',b')方向N會怎麼變化

當X_u和X_v正交時

「X_u和X_v」就是「X₁和X₂」

如果X_u和X_v沒有正交

雖然不是正交座標系

同樣可以用①來描述

沿著(a,b)方向N會怎麼變化

因為是linear & self-adjoint
所以①的dN_p矩陣一定可以被對角化 (why)
得到 ②

因為 ① = ② = ③
才會有 ➊ ➋ = ➌

圓柱體的 Ⅱp ( V )

好 這次的迷團是

方法1

第23講

方法2

為什麼結果對不起來，差了 1 / r²

再檢查1次

第2基本形式 = Normal curvature

幾何一 第19講C 17:00

這裡有要求要 Parameterization by Arc Length

| α'(s) | = 1

回去第2講找靈感

第2講

模仿第2講

驗算一下

現在 | X_t | = 1 了

Perfect

方法1

方法2

結果1樣

再整理一下

把 1 / r 從 a 移到 X_u

方法2

於是Ⅱ_p(V) = a² E k₁ + b² G k₂
又會變回Ⅱ_p(V) = a² k₁ + b² k₂

看起來

當「X_u和X_v正交」可以進1步讓

| X_u | = 1, | X_v | = 1

拿球來試看看

確實可以

dNp矩陣

有好多好多eg在這裡

在我們最熟悉的速食麵裡 🎶

前篇

如何用E、G、F、e、g、f

組裝出H、K

第24講

第24講

K：高斯曲率 K = k₁ × k₂

H：平均曲率 H = ( k₁ + k₂ ) / 2

k：主曲率分別是 k₁ , k₂

第24講

如何計算N

| X_u ^ X_v |怎麼來的

第15講

第15講

第15講

比較2種case

當X_u和X_v是正交基時

主曲率方向就是X_u和X_v

當X_u和X_v不是正交基時

主曲率方向不是X_u和X_v

好 這次的迷團是

「怎麼從H、K得出k₁ , k₂」

第23講
圖1

第23講
圖2

第23
圖3

這裡的dN_p是對角矩陣

第23講

當X_u和X_v是正交基時，dN_p才是對角矩陣

當X_u和X_v不是正交基時，dN_p就不是對角矩陣

第23講
圖4

所以

當X_u和X_v不是正交基時，dN_p不是對角矩陣

還可以從K、H得出k₁ , k₂嗎？

如果主曲率存在

用根與系數也能得到圖3的結果

高斯曲率 K = k₁ × k₂

平均曲率 H = ( k₁ + k₂ ) / 2

我懂了

當X_u和X_v不正交時

在Tangent space上

也能找出一組正交的向量(a₁ , b₁)和(a₂ , b₂)

這2個向量

就是矩陣A的Eigen Vector

特徵值分解
矩陣A =旋轉矩陣 × 對角矩陣 × (旋轉矩陣)^-1

進行特徵值分解後
就可以看到對角矩陣

於是

X_u和X_v不正交時的dX_p和dN_p可以改寫如下

(a , b)經過旋轉後變換到(a_pcs , b_pcs)

在principal curvature space裡

(1,0)會被map到 λ₁ (1,0)

(0,1)會被map到 λ₂ (0,1)

強化版

「怎麼從H、K得出k₁ , k₂」

第23講
圖1

修正：看來非對稱矩陣也可以

第23講
圖2

這裡的dN_p可以不是對角矩陣

第23講
圖4