好 這次的迷團是
|
|
出處 等式a |
|
| kx = θ |
當A、B、C是實數時
|
|
實數的case 完全難不倒我們的ChatGPT
|
當A、B、C是複數時
|
|
|
[ 等式左邊 ] 是 "橢圓上的點" 如果δ是實數，[ 等式右邊 ] 是 "線段上的點" "線段上的點"再怎麼也不可能 = "橢圓上的點" |
但如果δ是複數呢？
|
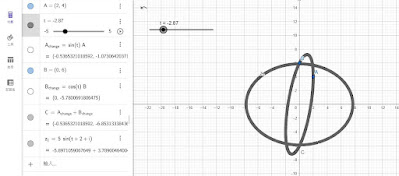
| 當x為複數，sin(x) 是一個橢圓 |
現在只要想辦法讓2個橢圓Match就行了
Round 1
無腦地使用上面的方法來找C和δ
|
|
顯然沒有完全Match
|
|
|
但如果把粉紅色橢圓透過旋轉和縮放來與黑色橢圓對齊 再找出2個phase的差 不就能完全Match了嗎？ |
Round 2
冷靜點
先回頭看一下sin(kx+δ)是什麼
|
|
這不就是橢圓嗎 cosh(β)和sinh(β)正是橢圓的長軸或短軸 |
而A cos(kx) + B sin(kx)形成的黑色橢圓
其長軸和短軸的比可能是任意 ≥ 1的值
如果
cosh(β)和sinh(β)的比也能是任意 ≥ 1的值的話
就可以用sin(kx+δ)還原出任意比例的黑色橢圓了
|
| 出處 |
|
|
出處 coth(x) = cosh(x) / sinh(x) |
是的它是
備註
 |
在Geogebra裡用coth-1(x)，它會自動換成tanh-1(1/x) 意思一樣 |
怎麼找出
A cos(kx) + B sin(kx)的傾斜方向？
這是1個求極值的問題
就是在找
讓 | A cos(kx) + B sin(kx) | 長度最短或最長的x
這種要懂很多三角函數的推導
我們還是看AI表演 🤠🍿🙂 That's tight
 |
正常的話，把θ代入A cos(θ) + B sin(θ) 就會得到極大值點E |
 |
| Geogebra Bcomplex < Acomplex時，E為極大值點 Bcomplex > Acomplex時，E為極小值點 備註 Bcomplex < Acomplex時，向量(B,C)會落在y軸右方 這時的C / B是arctan能處理的合法值 Bcomplex > Acomplex時，C / B和合法值剛好差1個負號 |
旋轉和縮放
|
|
Geogebra 把PinkOval旋轉和縮放後變成GreenOval |
修正相位
|
|
Geogebra 用內積找phase |
|
|
為什麼是 phase / 2 呢？ 為什麼座標沒有完全Match？ |
橢圓和圓不一樣
|
|
θ每次移動9度，可以發現點和點的間隔並不是固定的 所以不能直接用內積找phase |
|
| Geogebra |
θ差一個負號怎辦？
|
| Geogebra |
咻咻咻咻
用更直觀的方法
旋轉對齊
 |
| Geogebra 這1個Geogebra只能Match橢圓 沒有處理圓和線段的case |
極限值
 |
| 為了能Match圓，sin(t+βi)的長短軸比必須 = 1 這時β = ∞ 當β = ∞，sinh(β)和cosh(β)也是無限大 這時，sin(t+βi)是1個無限大的圓 |
 |
sin(t+βi)的長短軸比 = ∞ sin(t+βi)才能接近沒有厚度的線段 為了能Match線段，sin(t+βi)的長短軸比必須 = ∞ 這時β = 0 |
最後就用Kiss結束這1回合 🤠😗
沒有留言:
張貼留言