我可以喝酒不和你聯絡
任日子一天天這麼過 🎶

|
|
笛卡爾座標,基向量eu不隨位置改變 微分不用管eu項 |

|
|
極座標,基向量eu隨位置而變 微分要考慮eu項 |

|
| B-A = 2個座標系基向量的差 |

|
| 原圖來自這裡 |
a few days ago ...
張量tensor
要滿足這樣的形式
.JPG)
|
| 開放式課程 相對論 |
P-form
P-form是tensor的子集

|
|
P-form一定是Tensor
Tensor不一定是P-form
|
.jpg)
|
| covector是1-form |
對Tensor微分
結果不再是Tensor
有3種特別的微分能做到
1)李微分

3)協變微分
帶Γ的微分
對vector協變微分
Γ不是張量
它只是幫助張量成為張量
對covector協變微分
協變微分的幾何意義

|
| 泰勒展開 |

|
|
提出dxα到大括號外面,再除以E
就會得到下圖的綠色部分
|
+綠色項 VS +紅色項
有什麼差別?

|
|
原圖來自這裡
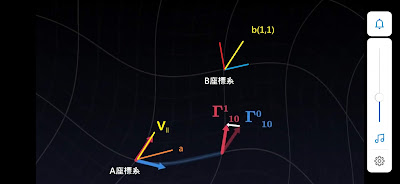
假設向量a和向量b長這樣
|
藍色項+綠色項 =
A座標系下的座標值(1,1)

|
|
原圖來自這裡 很明顯A座標系下的(1,1)和b的方向看起來不一樣 |
再+紅色項
會把(1,1)修正為V||
|
|
原圖來自這裡 A座標系底下的V||和B座標底下的b方向就一致了 |

|
| 圖① |
比較 圖①和圖②

|
| 圖② |
step by step
Γ長怎樣

|
| 原圖來自這裡 |

|
|
原圖來自這裡 |

|
|
原圖來自這裡 和教授的表示法不同
這個影片是用Γcex的話,教授就是用Γcxe
|

|
|
原圖來自這裡
Γcex的x指的是沿著那個方向微分
∂x0或∂x1
Γcex的e指的是對那個基向量微分
e0或e1
對基向量微分後
再變換回座標系A,結果為向量q e0 + r
e1
e0的座標值或e1的座標值
這就是Γcex的c
|
怎麼使用Γ

|
| Vα就是座標系A的向量a |
挖的麻吉置叨 🎶
置這 置這

|
| Demo |
我也好想要有被動收入 🙂🤠 等妳挖到石油
這女人很被動 不會主動touch
這女人很主動 都會主動touch
這收入很被動 會主動進我口袋
這收入很主動 不會主動進我口袋
發明被動收入這個人
是不是腦子不好使 🙂🤠 好球 觸殺出局



























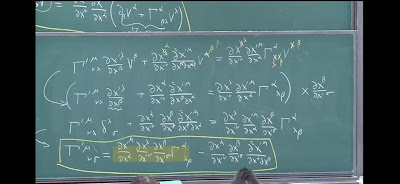















.jpg)


沒有留言:
張貼留言