dNp矩陣

有好多好多eg在這裡

在我們最熟悉的速食麵裡 🎶

前篇

如何用E、G、F、e、g、f

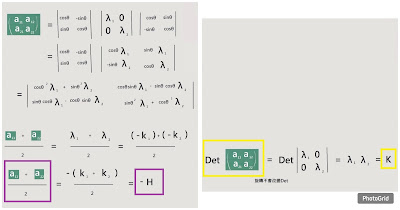
組裝出H、K

第24講

第24講

K：高斯曲率 K = k₁ × k₂

H：平均曲率 H = ( k₁ + k₂ ) / 2

k：主曲率分別是 k₁ , k₂

第24講

如何計算N

| X_u ^ X_v |怎麼來的

第15講

第15講

第15講

比較2種case

當X_u和X_v是正交基時

主曲率方向就是X_u和X_v

當X_u和X_v不是正交基時

主曲率方向不是X_u和X_v

好 這次的迷團是

「怎麼從H、K得出k₁ , k₂」

第23講
圖1

第23講
圖2

第23
圖3

這裡的dN_p是對角矩陣

第23講

當X_u和X_v是正交基時，dN_p才是對角矩陣

當X_u和X_v不是正交基時，dN_p就不是對角矩陣

第23講
圖4

所以

當X_u和X_v不是正交基時，dN_p不是對角矩陣

還可以從K、H得出k₁ , k₂嗎？

如果主曲率存在

用根與系數也能得到圖3的結果

高斯曲率 K = k₁ × k₂

平均曲率 H = ( k₁ + k₂ ) / 2

我懂了

當X_u和X_v不正交時

在Tangent space上

也能找出一組正交的向量(a₁ , b₁)和(a₂ , b₂)

這2個向量

就是矩陣A的Eigen Vector

特徵值分解
矩陣A =旋轉矩陣 × 對角矩陣 × (旋轉矩陣)^-1

進行特徵值分解後
就可以看到對角矩陣

於是

X_u和X_v不正交時的dX_p和dN_p可以改寫如下

(a , b)經過旋轉後變換到(a_pcs , b_pcs)

在principal curvature space裡

(1,0)會被map到 λ₁ (1,0)

(0,1)會被map到 λ₂ (0,1)

強化版

「怎麼從H、K得出k₁ , k₂」

第23講
圖1

修正：看來非對稱矩陣也可以

第23講
圖2

這裡的dN_p可以不是對角矩陣

第23講
圖4