看不懂的算法 是否來自太空
別人寫的代碼 看著像密碼 🎶
── Booming Tech。擎空
事情是這樣的
幾年前我買了一本
Jos Stam的The Art of Fluid Animation中譯本
|
| 隨書附上的 程式碼 |
陸陸續續讀了3遍
有2個地方就是看不懂
和書的內容對不上，分別是
- 壓力項：project函數
- 擴散項：diffuse函數
直到昨天看了
終於讓我找到關鍵的One Piece 🧐
拉普拉斯算子的離散形式
|
| GAMES103第11講 |
projection函數在做什麼？
 |
| GAMES103第11講 |
|
|
GAMES201第4講 u還不是不可壓縮的向量場 ∇•u ≠ 0 ( 水量分布不平均 ) 公式(5) u* = u - (Δt/Ρ) ∇p ∇p的存在會讓u變成不可壓縮的向量場u* ∇•u* = 0 ( 水量分布平均 ) 由此 推導出(8) 泊松方程 由泊松方程可知，當∇•u = 0 就不會有壓力差 ( ∇•∇p = 0 ) 沒有壓力差，∇p就是0向量 可見∇•u ≠ 0是造成∇p的起因 因果關系如下 水量分布不平均 ➡️ ∇p不是0向量 ➡️ 水量分布平均 |
|
|
GAMES201第4講 這是上面泊松方程的離散形式(有限差分) 解泊松方程可以得出壓力場p 再來就是解線性方程式，找出x A
x = b(x就是p) |
 |
Jos 在這裡做了一些優化 可以忽略Δt，因為那只是1個scale 當有一個線性方程組為 A x = (1/Δt) b忽略上式右邊的 (1/Δt)後，會有 A x = b得到的結果x 相當於預乘了Δt x = x Δt |
 |
| GAMES201第4講 有了p，就能算出不可壓縮的速度場u* |
|
上面2個步驟對映的程式碼
|
解泊松方程迭代的過程中
會使用到已更新的鄰居值
乍看之下會懷疑是不是程式碼寫錯了？
但它其實是在做 Gauss-Seidel迭代
就比較接近一般Programmer的想法了
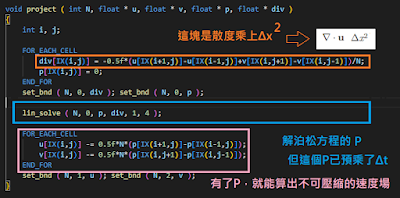
diffuse函數在做什麼？
diffuse 和 viscosity 有關
關於擴散項，一開始我們有
(ρ是流體密度，v = 黏滯系數/ρ)
a = v▽·▽u
假設
u 是當前速度
u' 是下一步的速度
u'' 是下下一步的速度
當前u + dt v▽·▽u
會得到下一步u'
u' = u + dt v▽·▽u
下一步u' + dt v▽·▽u'
會得到下下一步u''
u'' = u' + dt v▽·▽u'
反過來
u' - dt v▽·▽u' 就會得到u
u = u' - dt v▽·▽u'
移項後有
u' - u = dt v▽·▽u'
Δu = dt v▽·▽u'
這樣就和Jos的程式碼對上了
 |
| Δu = v▽·▽u' |
|
| 對映的程式碼 |
結語
此碼只應天上有？ 🤠🤔 人間能得幾回聞
補充資料
NS方程的幾何意義
|
|
From wiki ∇•v = 0代表流入 =流出 滿足∇•v = 0的流體就是不可壓縮流體 |
|
|
NS方程超清解說 太極圖形课S1第10講：流體仿真 01 |
沒有留言:
張貼留言