教材
中文參考資料
- Real-Time Polygonal-Light with LTC
- 基于 LTC 方法的 URP 实时多边形光源踩坑
- 利用LTC实现实时多边形面积光
- LearnOpenGL CN 区域光
- 实时范围光Area Light渲染及其数学原理推导
面光源對dA積分
可轉成對立體角dω積分
Do(ωo) ➝ D(ω)
Do(ωo) ➝ D(ω) ≃ p * cos(θi)

|
|
其實你愛我像誰 扮演什麼角色我都會 🎶 可愛又迷人的反派角色 🤠🙂 π米阿 |
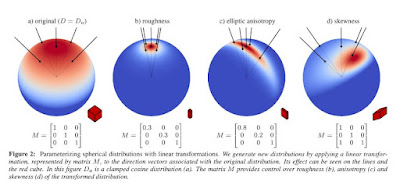
圖 a) 是Do(ωo)
Do(ωo)可以變成不同的D(ω)
圖 b) 是其中1種D(ω)
D(ω)又和 p cos(θi)長得很像
D(ω) ≃ p cos(θi) 代入式①後
get 式② Lo = L ∫
p cos(θi)
dωi = L ∫ D(ω) dω

|
|
出處
上方D(ω)
下方Do(ωo)
怎麼變換
先變換到shading point的Local space
(3軸是T1、T2、N)
再變換到Do(ω)空間
D(ω)的中心向量
會變成Do(ωo)的(0,0,1)向量
|
S是2個空間的bridge
Do(ωo) =
(1/π) cos(θo)
ωo是立體角,ωo是立體角的指向
有 S = ∫ Do(ωo) dωo
ωo和ω是「一一對應」
由上圖可知
Do(ω)分佈範圍大,D(ω)分佈範圍小
所以 dωo > dω
當濃度不變時 D(ω) = Do(ωo)
∫ D(ω) dω = ∫
D(ωo) dω < S
濃度提高後 D(ω) = Do(ωo)
dωo / dω
get 式③ ∫ D(ω)
dω = ∫ Do(ωo)
dωo = S

|
|
出處
上方D(ω)濃度高
下方Do(ωo)濃度低
把面光源的幾何形狀P
從D(ω)空間逆變換到Do(ω)空間後
Po會變大
|
怎麼找出dωo / dω
在Do(ωo)空間打光的好處
式② Lo = L ∫ p cos(θi)
dωi = L ∫ D(ω) dω
式③
∫ D(ω) dω
= ∫ Do(ωo)
dωo = S
由式②和式③可得
Lo = L ∫ p cos(θi)
dωi
= L ∫ Do(ωo) dωo = L S
Do(ωo) =
(1/π) cos(θo)
∫ Do(ωo)
dωo = ∫ (1/π) cos(θo) dωo
S = (1/π) ∫ dω⊥o
Lo = L ∫ p cos(θi)
dωi
= L ∫ Do(ωo) dωo = L S = L
(1/π) ∫ dω⊥o
在另Do(ωo)空間進行打光
只要積分投影立體角!
積分投影立體角
E(Po) = S= ∫ Do(ωo)
dωo = (1/π) ∫ dω⊥o
嚴格說來 ∫ Do(ωo) dωo 其實不是Irradiance E
使用
結束這1回合

|
Bravo! |