半球積分與面光源積分 🐞

➡️ 目錄

開端

故事的開端是，我看了網上的LearnOpenGL CN 光照
在讀程式碼的時候，嗅到了1些不對勁

程式碼片段，來自LearnOpenGl CN 光照

於是我開始展開調查
這麼說來，我小時候的夢想，就是想做個警探呢...
(有點像Jacky的電影那樣，不是像現在這種版本)

如果你覺的這隻馬很面熟
對他叫熱鬥小馬，不是我原創的

後來我漸漸明白，「L的定義」再加上「BRDF的定義」，
從這2個地方出發，可以得到渲染方程

L是什麼？

我們從L的定義出發，真實世界只有面光源
但遊戲世界充滿了點光點，所以先看點光源

• 點光源的L 👩‍🔬

再來是面光源

• 面光源的L 
• L_c  = dE / ( dω cos(θ_o) )

除以cos(θ_o)，是為了讓每個方向的L都是定值
計算光照時，會再考慮cos(θ_o)的影響

入射光源的Cos(θ_i)項

ΔA_s 是 shading point的微小面積

能全部擊中shading point dA_s的是dE_i

Integrals over Area 式(5.6)

Integrals over Area
E = ∫ dE
出處

dω_i = cos(θ_o) dA / r ² 
dE⊥ = L dω_i
dE = cos(θ_i) L dω_i

使用L_o = L_c * cos(θ_o) 
dE_i =cos(θ_i) L_o dω
dω = dA / R_i ² 
也能推導出同樣的結果

渲染方程半球積分的dω

當初被點光源帶偏了

怎麼都想不通為什麼dω要從ΔA_s的視角出發

於是我認為半球積分裡需要 (1 / R_i ²) 項

半球積分裡多了 (1 / R_i ²) 項 🐞

修正 🐞：

• 半球積分的1/(R*R)？ ⭐⑤
• 半球積分的Li dωi ⭐⑥

現在，讓我們回到故事的開端

重新檢視LearnOpenGL CN 光照的程式碼
橘色圈起來的那個
其實應該叫irradiance (會隨距離衰減的E⊥_i)

• 點光源的謎團 ⭐

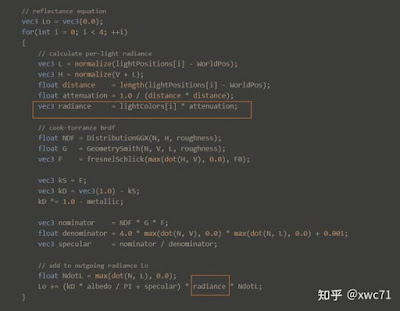
程式碼片段，來自LearnOpenGl CN 光照