連續 VS 光滑
連續不1定光滑(可微)
但光滑(可微)1定連續
 |
左邊2個線段是光滑又連續 右邊2個線段連續但不光滑(出現尖點) |
Regular Surface
 |
| 出處:幾何一 第7講 池同學的筆記 |
條件①和條件②在看
surface是不是連續
map X
是不是可逆和對射(1-1 & onto)
條件③在確認surface
是否在切平面上所有方向都是光滑的
對射(1-1 & onto)
 |
| S1:平面 S2:捲起來的平面 |
莫比烏斯帶
只用幾何一 第17講給的判定條件
看不出來為什麼莫比烏斯帶不是可定向
 |
| 出處:幾何一 第17講 張同學的筆記 |
必須再加上1個判定:
同1點是不是只有1個法向量
 |
| 出處 |
可定向Surface
同1點只會有1個法向量
不可定向Surface
同1點可能有2個法向量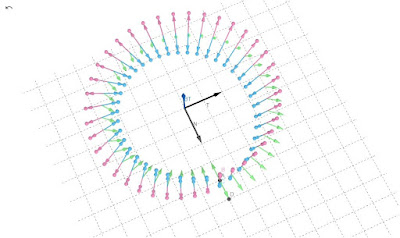 |
點A有2個法向量 所以是不可定向 |
Monument Valley style
 |
| 帶子 小人版 |
沿著中間剪開
 |
左:邊邊轉0圈後黏在1起 右:邊邊轉0.5圈後黏在1起 |
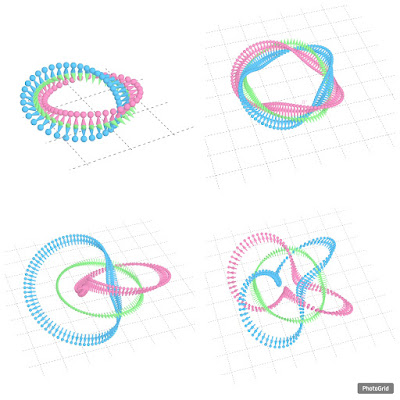 |
| 左:邊邊轉1圈後黏在1起 右:邊邊轉2圈後黏在1起 左:藍帶子會穿過粉紅帶子中間的洞1次 右:藍帶子會穿過粉紅帶子中間的洞2次 |


.png)

.png)


沒有留言:
張貼留言