像我
punchline
每句都是有道理
都是重點 每句都畫螢光筆 🎶
 |
| 出處 |
 |
| 出處 |
 |
| 出處 |
小蛋嘉 🙂🤠 你放莊重1點
方向導數、梯度
 |
| 出處 |
不懂,那就中華一番
 |
| 出處 |
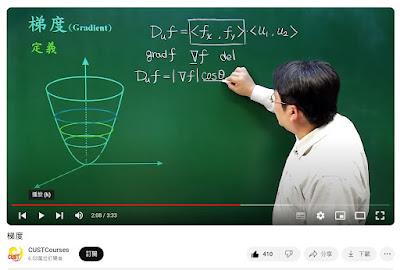
梯度
∇f為向量
指出往那個方向,方向導數最大
 |
| 出處 |
散度
A為向量
∇。A為純量
 |
| 出處 |
上面的數學描述就是物理學家說的Tiny Cube
 |
| 出處 |
散度>0 ⇔ 流出
散度<0 ⇔ 流入
拉普拉斯
f為純量
∇。∇f為純量
 |
| 出處 |
 |
| 這麼喜歡貼貼紙 🤠🙂 不要小看包裝 |
拉普拉斯就是Tiny Cube和鄰居比大小
旋量、旋度
當C為z軸平面上的正方形路徑
 |
| 出處 |
 |
| 出處 正方形的dxdy = dS curl E。n = ∇xE。n 用x軸平面上的正方形路徑,可以得到∇xEx
用y軸平面上的正方形路徑,可以得到∇xEy
|
旋度
∇xV為向量
借鏡梯度
旋度指出旋量最大的平面軸N
一般化
用來對付那些
放飛自我(可以隨意轉動)的小方塊
 |
| Binormal,还是Bitangent,这是个问题 💫 |
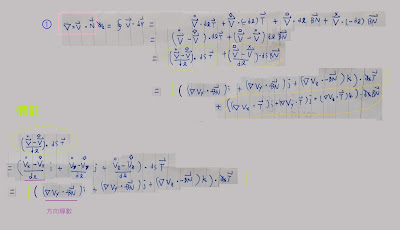 |
|
還好不用真的和sin cos打交道 😋
方向導數現學現賣? 🤠
|
當C不是正方形路徑
比如像是梯形
 |
|
計算完會發現dS = (3/4) dxdy
和正方形的dS = dxdy 相比
多了1個形狀因子Area Factor A
這個case裡A就是(3/4)
|
 |
| 可見路徑不影響最後的結果 |
🎁
0維的點包1維的線
1維的線連通成1維的環
1維的環包2維的面
2維的面連通成2維的球面
2維的球面包3維的體
3維的體連通成3維的?
3維的?包4維的?
出發就走得到 來時路不會被 剪斷 🎼
 |
| 誰收到這種生日禮物會開心?🤠🙂 |
 |
| 別多想就是直接做 哪來的美國時間拖 如果沒膽先吃些蔥 就啵吧 就啵吧 🎶 給你相相 🤠🙃 我不要 |
 |
| 我不愛念書
只想練功夫 如果我會輕功真酷 🎶 ☂️ 水里 谷山 |
 |
| Powered By
FaceApp |
























沒有留言:
張貼留言