金秘書Contact Info為何那樣?
again 在這篇文章看到下面這張圖
|
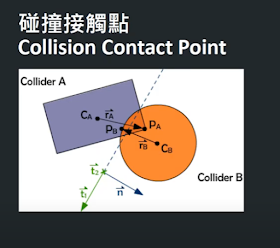
| 圖1 |
第1時間不太明白為何Contact Tangent長那樣?
還有Coliider B的Contact Point 為何是PB?
只好請出Google 翻譯
發現不少上次沒注意到的細節(知識綠洲) 🧐
GJK的適用對向
之前以為GJK只能用在2個凸多邊形
但其實它可以用在2個凸集
Minkowski差
就是下面的黃色區域
在Allen Chou的文章裡又把它稱為CSO
GJK的核心思想
2D版:
不需要一開始就建立整個CSO
而是利用Support Function逐步擴展Simplex
點 ⏩ 線 ⏩ 三角形
如果三角形如果包含原點
就代表2個凸集交疊
否則就退化回到線
再重新擴展成三角形
詳細過程可以參考這篇文章GJK
3D版:
利用Support Function逐步擴展simplex
點 ⏩ 線 ⏩ 三角形 ⏩ 四面體
如果四面體如果包含原點
就代表2個凸集交疊
否則就退化回到三角形
再重新擴展成四面體
為什麼叫Support Function?
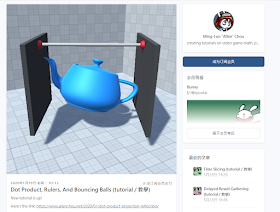
再次借用Allen Chou另一篇文章的圖片
|
|
兩本平行的書不斷靠近 最終可以夾住中間的茶壺 這不就是Support(支撐)嗎 |
類似上圖,Support Function(v)的目的是
找出CSO沿著某個方向的最遠端點
使用Support Function即使不知道CSO的全貌
也能做到上面說的:逐步擴展simplex
CSO邊界和原點的最短距離
case 1
找出CSO邊界上和原點最靠近的最近邊 (黃色區域左下方的粉紅邊)
就可以得到最近點(和原點最接近)

|
| 紫色是最近距離 |
如同最近點是最近邊上的內插點
最近點是邊AD上的內插點
最近點就是Collider A的Contact Point
有了最近點,再移動紫色距離
就可以得到Collider B的Contact Point ➡️
F
case 2
找出CSO邊界上和原點最靠近的最近邊 (黃色區域左上方的淡藍色邊)
就可以得到最近點
如同最近點是最近邊上的內插點
最近點是邊FG上的內插點
最近點就是Collider B的Contact Point
有了最近點,再移動紫色距離
就可以得到Collider A的Contact Point ➡️
A
EPA(Expanding Polytope Algorithm)
2D版:
利用GJK找到的Simplex
逐步擴展成包含最近邊的Polytope
Simplex是三角形
Polytope是凸多邊形
詳細過程可以參考這篇文章EPA
3D版:
利用GJK找到的Simplex
逐步擴展成包含最近三角形的Polytope
Simplex是四面體
Polytope是凸多面體
CSO邊界和原點的最短距離(圓形vs多邊形)
前面提到EPA主要在找出最近邊
但在下面這種case
最近邊是圓弧上的點

|
| 玩看看 |
我用EPA試了一下
人工迭代幾次之後,發現似乎可以用圓形來加速 🤔
用圓形加速
既然最近邊是圓弧上的點
那就直接使用圓形來找出最近點!

|
| 圓點在圓形內的case |

|
|
圓點在2個圓形內的case 最近點找距離大的那個 |

|
| 圓點不在圓形內的case |
但在這些case還需要額外的判定

|
|
case A 原點在圓內,但最近邊不在圓上 (最近邊和邊AB平行) 玩玩看 |
在上面這個case
原點投影到最近邊的投影點合法(投影點位在藍色最近邊內)
所以藍色最近邊是最近邊
粉紅色投影點是最近點

|
|
case B 原點在圓內,最近邊在圓上 玩玩看 |
在上面這個case
原點投影到最近邊的投影點不合法
所以藍色最近邊不是最近邊
紅色點才是最近點
現在,終於可以回到本篇一開始的問題
Contact Info為何那樣?
比對實驗結果
不管是case A還是case B
2個Contact Point的連線(紫色線段)方向,就是contact Normal的方向
2個Contact Point和右邊Collider的圓心會3點共線
2個Contact Point和右邊Collider的圓心會3點共線
但圖1裡2個Contact Point分別是PB、PA
PB、PA的連線方向,和contact Normal不一樣
2個Contact Point和右邊Collider的圓心也沒有3點共線
互換Collider B和Collider A
多邊形是Collider B、圓形是Collider A
土黃色是 Support(v,A) + Support(v,-B)
草綠色是 Support(v,B) + Support(v,-A)
看起來2種結果只是差在
沿著x軸進行一次鏡像、況著y軸進行一次鏡像
結語
2天前本來要放棄的我
回過神,現在又在這裡了 ⛳
有一種淡淡(蛋蛋)的味道叫做幸福 😋🤠 荷包蛋 like